Herleitung zu "Ziehen einer Wurzel per Hand"
|
Für die Herleitung des Verfahrens soll beispielhaft die Wurzel aus 5776 gezogen werden. Diese Wurzel liefert das zweistellige Ergebnis 76, auf das die Herleitung aufbaut. Ein- und mehrstellige Ergebnisse lassen sich dann analog ableiten.
Um die Herleitung besser nachvollziehen zu können, ist es hilfreich zunächst einmal die Wurzel aus 5776 nach dem beschriebenen Verfahren zu ziehen und dann die Herleitung durchzugehen.
Die Annahme... |
|
Ausgehend von einem 2-stelligen Ergebnis kann man folgendes schreiben (1.1).
n und m können dabei jeweils die Ziffern 1 bis 9 sein.
(1.1)
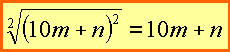
Wendet man nun die Binomische Formel (2.1) unterhalb der Wurzel an, so ergibt sich (2.2).
(2.1)
(2.2)
Das Beispiel... |
|
Für das Beispiel (3.1) ergibt sich daher Gleichung (3.2) und zusammengefasst Gleichung (3.3).
(3.1)
(3.2)
(3.3)
Der Ansatz zur Lösung... |
|
Für die Findung der Lösung sind die 2 Unbekannten m und n zu ermitteln (4.1). Deshalb setzt man die zu radizierende Zahl, also die aus der die Wurzel gezogen werden soll (hier 5776), mit dem Term unter der Wurzel aus (2.2) gleich und erhält (4.2).
(4.1)
(4.2)
Anhand dieser Gleichung (4.2) ist nun im ersten Schritt m und im zweiten Schritt n zu ermitteln, wie im Folgenden beschrieben.
Der erste Schritt zur Lösung: Ermitteln von m... |
|
Im ersten Schritt soll die Unbekannte m gefunden werden. In der Gleichung (4.2) taucht m zum einen im Term (5.1) und zum anderen im Term (5.2) auf. Im Term (5.3) ist m nicht vorhanden.
(5.1)
(5.2)
(5.3)
Um nun ein m zu finden, welches dem Term (5.1) entspricht, verwendet man als Hilfsmittel folgende numerische Reihe (6.1), welche besagt, dass das Quadrat einer Zahl z gleich der Summe aller ungeraden Zahlen kleiner 2z ist. Die Anzahl der Summanden in dieser Reihe entspricht somit auch der Zahl z.
In (5.1) handelt es sich aber um ein Quadrat mit 100 multipliziert, so dass man die Reihe entsprechend erweitern muss (6.2).
(6.1)
(6.2)
Versucht man nun gemäß (6.2) die Summe ungerader und mit 100 multiplizierter Zahlen zu finden, die gerade noch in die zu radizierende Zahl 5667 passt, erhält man mit der Anzahl der Summanden die gesuchte Zahl m. Das Vorkommen von m im Term (5.2) kann dabei außer acht gelassen werden, da es gegenüber den Summanden der Reihe (6.2) nicht ins Gewicht fällt.
Im Folgenden werden nun die Summanden der Reihe (6.2) solange unter die zu radizierende Zahl 5667 geschrieben, wie deren Summe diese noch nicht übersteigt. Im beschriebenen Verfahren zum Wurzelziehen, werden die Nullen (00) der Übersichtlichkeit halber weggelassen.
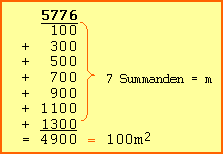
Als Ergebnis erhält man nun die Summe 4900 und die Anzahl der Summanden, welche 7 beträgt. Die gesuchte Zahl m ist somit 7.
Gemäß dem Term (5.1) muss das Quadrat von m mit 100 multipliziert auch die erhaltene Summe 4900 ergeben, was der Fall ist.
Der zweite Schritt zu Lösung: Ermitteln von n... |
|
Der Term (5.1) und somit m sind im vorangegangenen Schritt ermittelt worden. Term (5.2) der ebenfalls m enthält, kann somit auch vereinfacht werden. So ergibt sich die vereinfachte Gleichung (7.1), die im 2. Schritt zur Findung von n verwendet wird.
(7.1)
Die Gleichung (7.1) muss nun umgestellt werden, indem die im vorigen Schritt ermittelte Summe 4900 von der zu radizierenden Zahl 5776 abgezogen wird. Im beschriebenen Verfahren bildet man dazu den Rest von 56 und 49, der gleich 8 ist, und zieht die nächsten 2 Stellen 76 herunter. Dadurch ergibt sich 876. Gleichung (8.1) stellt die umgestellte Gleichung dar.
(8.1)
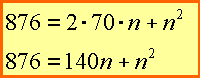
In dieser Gleichung (8.1) taucht nun n im Term (9.1) mit 140 multipliziert und im Term (9.2) quadriert auf. Die Zahl 140 entspricht dabei dem bisherigen Ergebnis m=7 verdoppelt und mit 10 multipliziert (um eine Stelle nach links verschoben), wie es im beschriebenen Verfahren praktiziert wird.
(9.1)
(9.2)
Um nun n zu ermitteln, nutzt man zum einen wieder die numerische Reihe (6.1) für den Term (9.2) und zum anderen die Anzahl der Summanden für den Term (9.1). Mit anderen Worten, man sucht wie oft die Zahl 140 (9.1) und das Quadrat dieser Anzahl (9.2) in den verbliebenen Rest 876 passt (10.1).
(10.1)
Man schreib also nun kombiniert jeweils 140 und einen weiteren Summanden der numerischen Reihe (6.1) unter die Zahl 876; und das solange, wie deren Summe die Zahl 876 nicht übersteigt.
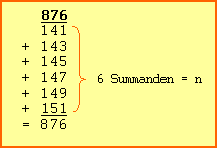
Die Anzahl der Summanden ist nun wieder die gesuchte Zahl n = 6.
Da die Differenz aus 876 und der ermittelten Summe 876 gleich 0 ist, ist die Lösung hiermit komplett.
Die Lösung... |
|
Die Lösung ist nun durch die gefundenen Zahlen m = 7 und n = 6 gegeben. Im beschriebenen Verfahren schreibt man die gefundenen Ziffern der Reihe nach hinter das Istgleich-Zeichen und erhält 76.
Für die Formel aus dem Ansatz (4.1) ergibt sich das gleiche (11.1)
(11.1)
© 2000-2004 Andreas Göbel Impressum · Datenschutz/Cookies
Casio Polynomdivision
Fotos
Kalender Übersicht
Mathematik Übersicht
Impressum - Datenschutz/Cookies
Kalender
P.M. Logiktrainer
Römische Zahlen
Deutsche Schrift, Sütterlin
Wochentage im Kopf
Transkription
Wurzel Herleitung
Wurzel
Wortwoertlich
Deutsche Verbformen generieren
Verbformen generieren, konjugieren